技术综述|实体对齐技术概述-k8凯发旗舰

实体对齐的目标是从描述真实世界对象的两个不同的知识图谱中识别出等价实体对。等价实体对是指描述客观世界中同一事物但来自不同知识图谱的两个实体，如图1中的“成龙”和“陈港生”。实体对齐可以将不同图谱间的实体进行合并，从而将不同来源的知识关联起来，形成大而全的知识图谱，为后续的任务（如智能问答等）提供更丰富全面的知识。

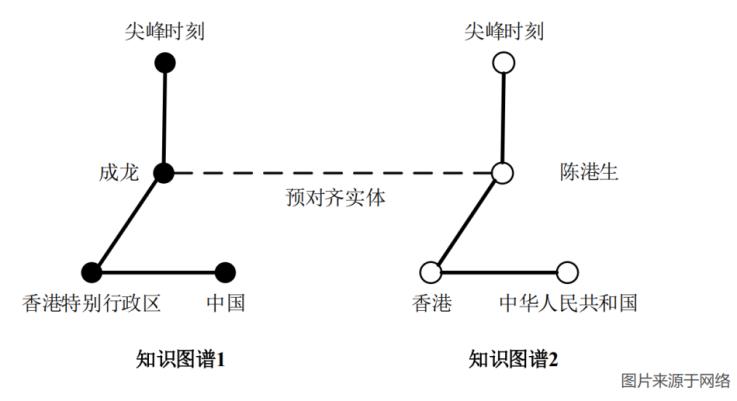
图1 实体对齐任务示意图

在现有研究中，基于嵌入的实体对齐方法可以分为基于翻译的实体对齐方法和基于图神经网络的实体对齐方法[1]。这两类方法都是通过生成实体的嵌入并计算向量间的相似度来衡量实体的相似性，从而完成实体对齐。

一、基于嵌入的实体对齐方法通用框架

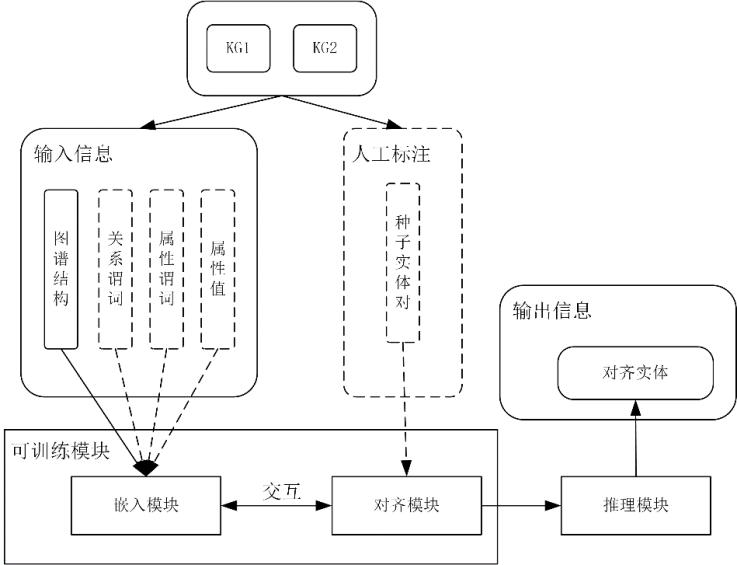
图2 基于嵌入的实体对齐方法通用框架

一般而言，基于嵌入的实体对齐方法可以用统一的框架来进行描述，如图2所示。其中，虚线框代表该组件是可选的。基于嵌入的实体对齐方法的输入为图谱结构、关系谓词、属性谓词和属性值。其中，图谱结构由关系三元组（头实体，关系，尾实体）表示；关系谓词、属性谓词和属性值是可选的。实体对齐包含三个模块：嵌入模块、对齐模块和推理模块。

嵌入模块旨在生成嵌入向量表示。其输入为图谱结构、关系谓词、属性谓词和属性值，用于生成实体嵌入、关系嵌入和属性嵌入。在所有可能的输入中，图谱结构是最基本且最重要的输入，包含了图谱的结构信息。其他类型的信息（关系谓词、属性谓词和属性值）通常以自然语言短文本的形式表示，其中包含丰富的语义信息，这可能有利于实体对齐。嵌入模块会分别计算图谱1和图谱2的实体嵌入，使图谱1和图谱2的嵌入分别落入不同的向量空间。

对齐模块旨在将嵌入模块对图谱1和图谱2各自生成的嵌入向量统一到同一个向量空间中，以便识别对齐的实体。这是实体对齐面临的主要挑战。实体对齐技术一般使用一组人工标注的等价实体对作为训练集来训练对齐模块。这种人工标注的等价实体对被称为种子实体对。

推理模块旨在判断图谱1和图谱2中的一对实体是否对齐。一般而言，可以根据对齐模块获得的嵌入向量，对图谱1中的每一个实体使用最近邻搜索算法来计算图谱2中与之相似度最高的实体，组成一个对齐实体对。常用的相似性度量包括余弦相似性、欧几里得距离等。

二、基于翻译的实体嵌入对齐方法

基于翻译的实体嵌入对齐方法的思想是将知识图谱中的关系视为从头部实体嵌入到尾部实体嵌入的“翻译”。transe[2]是第一个基于翻译的嵌入模型，它将实体和关系嵌入到统一的向量空间中。其主要思想是：如果能够找到一套实体和关系的完美向量表示，那么对于任何正确的关系三元组(h,r,t)，相应的头实体嵌入h、关系谓词r和尾实体t应该满足h r=t的向量转换操作。例如，对于三元组（中国，首都，北京）而言，“中国”的嵌入加上“首都”的嵌入应该等于“北京”的嵌入。因此，学习的目的是找到一组嵌入，通过拟合的方式使图谱中所有关系的三元组之和最小。

对于属性信息，也可以采用类似的方式寻找“翻译”。如attre[3]使用公式h a-t(v)计算实体的属性。其中h是实体，a是属性谓词，v是属性值，t(v)是使用聚合n-gram的字符嵌入。attre在原有关系信息的基础上引入了属性信息，使得实体嵌入距离所有关系三元组和属性三元组的距离之和最小。

三、基于图神经网络的实体嵌入对齐方法

图神经网络（graph neural network, gnn）直接适配知识图谱固有的图形结构。基于gnn的实体对齐方法一般使用图注意力网络（graph attention network, gat）或图卷积神经网络（graph convolutional network, gcn）作为嵌入对齐模型。基于图谱对齐的实体往往具有相似邻域和属性的特性，图神经网络模型可以将邻域实体嵌入进行融合，从而使实体嵌入具备邻域信息。

在将图谱输入到gnn模型中时，一般需要构建图的邻接矩阵和特征输入矩阵。这类方法通常通过图谱的关系三元组构建图谱的带权邻接矩阵，从而指导模型有选择性地融合邻域实体。例如，gcn-align[4]分别计算一个关系r连接的头实体的数量和尾实体的数量，然后分别除以包含关系r的三元组的数量并相加，以此作为关系r的权重。

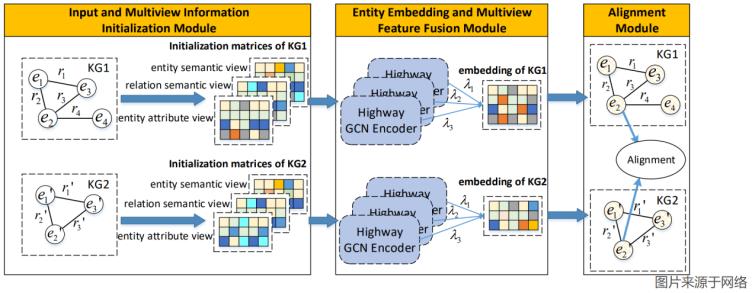
图3 mhgcn多特征视图结构

考虑到图谱的不同特征，特征输入矩阵一般使用多个视图融合，如mhgcn[5]从实体语义、关系语义和实体属性的角度构建了三个视图，并通过gcn将多个视图的特征进行融合，生成最终的实体嵌入，如图3所示。

参考文献

1. r. zhang, b. d. trisedya, m. li, y. jiang, and j. qi, “a benchmark and comprehensive survey on knowledge graph entity alignment via representation learning,” the vldb journal, vol. 31, no. 5, pp. 1143-1168, 2022.
2. a. bordes, n. usunier, a. garcia-duran, j. weston, and o. yakhnenko, “translating embeddings for modeling multi-relational data,” advances in neural information processing systems, vol. 26, 2013.
3. b. d. trisedya, j. qi, and r. zhang, “entity alignment between knowledge graphs using attribute embeddings,” in proceedings of the aaai conference on artificial intelligence, 2019, vol. 33, no. 1, pp. 297-304.
4. z. wang, q. lv, x. lan, and y. zhang, “cross-lingual knowledge graph alignment via graph convolutional networks,” in proceedings of the 2018 conference on empirical methods in natural language processing, 2018, pp. 349-357.
5. j. gao, x. liu, y. chen, and f. xiong, “mhgcn: multiview highway graph convolutional network for cross-lingual entity alignment,” tsinghua science and technology, vol. 27, no. 4, pp. 719-728, 2021.

总编：黄翰

责任编辑：刘廷辉

文字：朱浩锋

图片：朱浩锋

校稿：何莉怡

时间：2023年7月10日