该论文来自” ieee transactions on neural systems and rehabilitation engineering”期刊, 发表于 2021 年 1 月 16 日, 论文名称为”cross-disciplinary emotion recognition based on similarity of eeg signal transfer learning domain”.
为了解决通过脑电图(eeg)信号迁移学习进行跨被试情绪识别中由于源域数据的负迁移而导 致的准确率下降问题, 这篇论文提供了一种新的方法来动态选择适合迁移学习的数据, 并消除可能导致负迁移的数据. 这种方法被称为跨被试源域选择(cross-subject source domain selection, csds).
改论文提出的方法主要分为三个部分. 首先, 根据 copula 函数理论建立 frankcopula 模型, 用于研究源于和目标域之间的相关性, 用 kendall 相关系数来描述. 然后改进了最大平均差异的计算方法, 以确定单个源中类之间的距离. 归一化后叠加肯德尔相关系数, 并设置阈值已识别最合适迁移学习的源于数据. 最后在迁移学习的过程中, 在流形嵌入分布对齐的基础上, 使用局部切线空间对其方法对非线性流形的局部集合进行低维线性估计, 保持了降维后样本数据的局部特征. 最后的实验结果表明, 与传统方法相比, csds 方法使情绪分类的准确率提高了约 2.8%, 运行时间缩短了 65%.
方法介绍
他们首先提出使用 copula 函数对跨受试者脑电信号之间的非线性相关性进行建模并设置权重,然后通过改进的最大均方差(mmd)方法将源域数据集的权重相加,对源域数据进行滤波,以更好地传输滤波后的数据。最后,基于 meda,他们提出了一种迁移学习方法,该方法在将数据投影到流形空间时,在降维过程中使用局部切线空间对齐(ltsa)来保持数据的原始空间结构,以提高分类精度。

copula 函数也被称为连接函数,用于描述多个变量之间的所有相关性。
f 是 d 维随机变量![]() 的联合分布函数,对应的边分布为
的联合分布函数,对应的边分布为![]() ,c()是 d 元 copula 函数,使得所有
,c()是 d 元 copula 函数,使得所有 ![]() 。
。
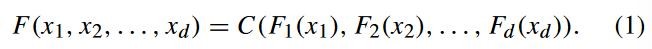
设随机变量 ![]() 对应的连续分布函数为
对应的连续分布函数为![]() , 可以得到
, 可以得到![]()
。它服从[0,1]的均匀分布,随机变量 ![]() 的联合分布是:
的联合分布是:
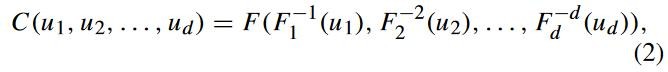
![]() 是
是![]() 的伪逆数,被定义为:
的伪逆数,被定义为:
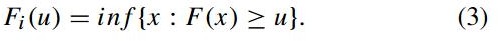
假设 n 维向量 ![]() 的边缘密度函数为
的边缘密度函数为![]() ,copula 函数的密度为:
,copula 函数的密度为:
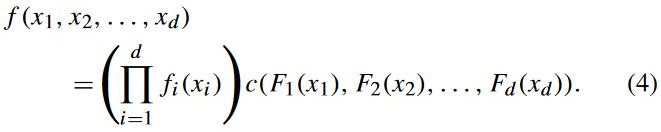
两个随机变量的连续累积分布是指分别对两个服从[0,1]均匀分布的随机变量应用概率积分变换得到的分布,它们的相关性可以用变换后的分布的相关性代替。然后,它被简化为在两 个均匀分布上定义联合分布,这是一个 copula 函数,分为三种类型:阿基米德型、椭圆型和二次型。
对于脑电信号的情绪模型,不同受试者在不同时间的脑电图像是不同的。当使用 copula 函数建模时,样本分布函数和概率密度不能被清楚地假设;因此,非参数估计不假设基本分布, 而是主要利用随机样本的信息来判断估计器的优缺点,这适合于 eeg 信号建模。
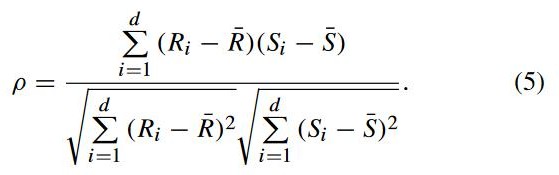 spearman 相关系数ρ也被称为秩相关系数,使用两个变量的秩进行线性相关分析:
spearman 相关系数ρ也被称为秩相关系数,使用两个变量的秩进行线性相关分析:
![]() 和
和![]() 分别表示 x 和 y 的秩,
分别表示 x 和 y 的秩,![]() 和
和 ![]() 分别代表
分别代表![]() 和
和![]() 的等级,越大相关性越强。
的等级,越大相关性越强。
肯德尔相关系数τ表示分类变量的统计数据,它用于反映分类变量的相关性,适用于两个分类变量按顺序分类的情况。
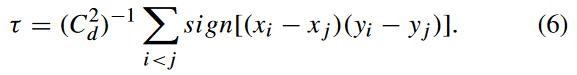
其中,![]() 代表观测数据。τ越大,变量之间的相关性更高。
代表观测数据。τ越大,变量之间的相关性更高。
mmd 是衡量两个分布在重现核希尔伯特空间中的距离。它是一种内核学习的一种方法。定义为:
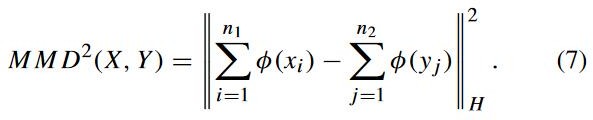
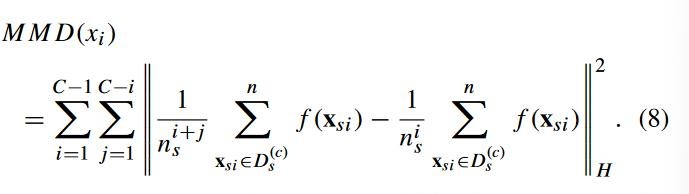
![]() 表示原始数据到希尔伯特空间的映射。这个公式用于确定核空间中两堆数据之间的平均 距离。作者提出了改进的 mmd 公式,用于计算源域中类间距离的总和。
表示原始数据到希尔伯特空间的映射。这个公式用于确定核空间中两堆数据之间的平均 距离。作者提出了改进的 mmd 公式,用于计算源域中类间距离的总和。
c 表示源域内的类别,![]() 表示单个源域中类别之间的距离。如图 1 是分两类结果核源域中类间距离之和的相关性,可以看到类间距离之和越大,对应的准确率越高。
表示单个源域中类别之间的距离。如图 1 是分两类结果核源域中类间距离之和的相关性,可以看到类间距离之和越大,对应的准确率越高。
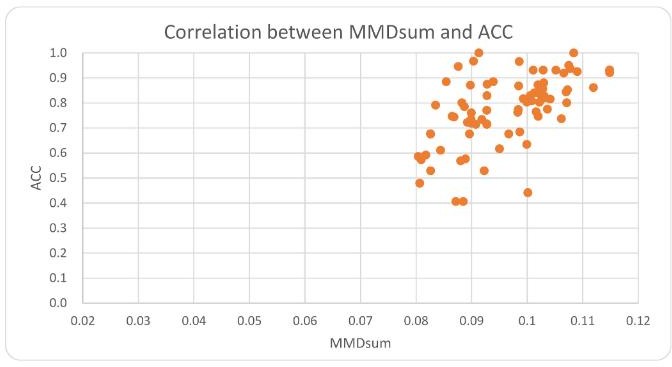
图 1
不同的源域被赋予不同的置信度,叠加上文中 copula 相关系数的置信度来筛选数据迁移学习的源域。
在传统特征匹配的领域自适应方法中。条件分布和边际分布的重要程度是不相等的,在原始 空间对齐分布会导致其特征的失真。这种效果并不理想。新的研究中提出了一种避免特征失 真并定量估计边缘分布和条件分布的重要性的方法。首先,为了消除退化的特征,流形特征 泛函 g(.)是在格拉斯曼流形 g(d)中研究的,引用测地流核(the geodesic flow kernel,gfk)来
促进其域适应。
动态分布的目的是定量评估两种分布在域适应中的重要性:
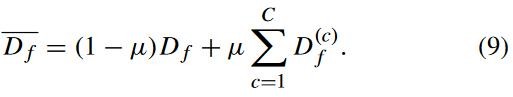
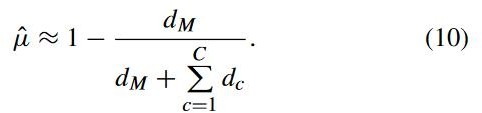
![]() 是自适应因子,
是自适应因子, ![]() 代表边际分布,
代表边际分布,![]() 代表条件分布,c 代表类别。通过计算距离 a 的自适应来平衡两种分布的重要性:
代表条件分布,c 代表类别。通过计算距离 a 的自适应来平衡两种分布的重要性:
其中, ![]() 代表边界 a 距离, 代表某个类的距离。通过 srm 的原理总结可以得出损失函数:
代表边界 a 距离, 代表某个类的距离。通过 srm 的原理总结可以得出损失函数:
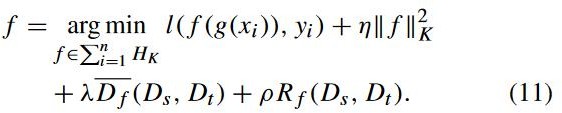
![]() 代表 f 的平方范数,
代表 f 的平方范数,![]() 代表动态分布对齐,
代表动态分布对齐, ![]() 代表拉普拉斯正则化,η、λ和ρ是正则化参数。
代表拉普拉斯正则化,η、λ和ρ是正则化参数。
一般的降维方法涉及目标数据的降维映射,以获得高维数据的低维表示。线性方法,如主成
分分析(pca)通常用于流形嵌入部分,以降低数据的维度。数据投影后,数据的局部结构不 应改变,ltsa 方法可以用于降低数据的维度。首先,用邻域表示局部非线性几何性质。首先,给出一个含有噪声的潜在非流形结构的样本数据集。其目的是通过最小化全局重建误差
来获得全局坐标。 ![]() 是重构残差,
是重构残差, ![]() 表示在样本点的 k 个邻域范围内有 pca 但没有降维的样本数据,
表示在样本点的 k 个邻域范围内有 pca 但没有降维的样本数据, ![]() 表示局部未知的仿射变换。
表示局部未知的仿射变换。
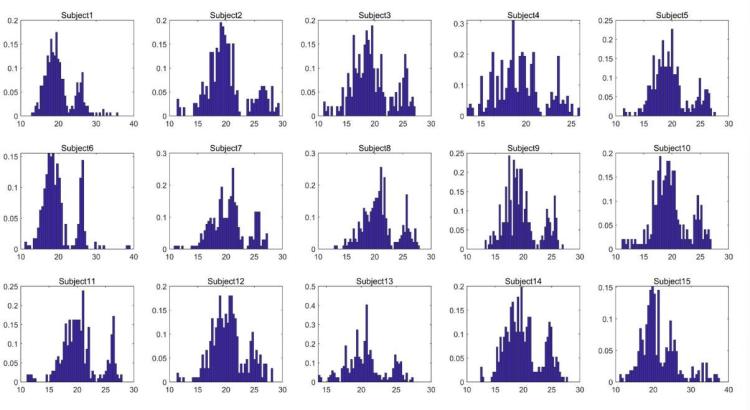
图 2
不同受试者的频率直方图的差异比同一受试者的不同数据更显著。简化的过程如图 2 所示, 图中显示了不同受试者的数据差异,从数据的分布可以看出明显的差异。
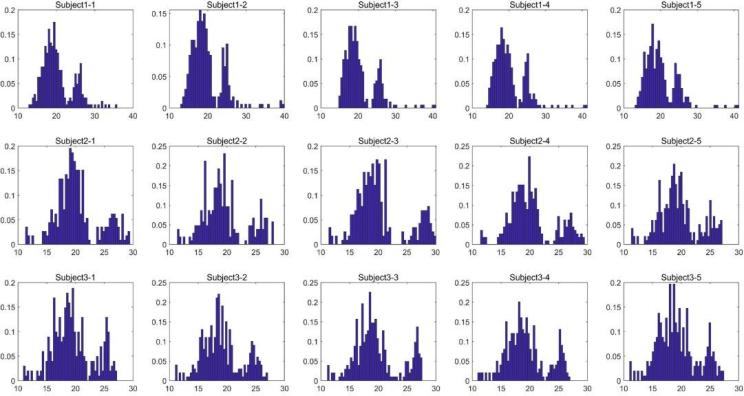
图 3
图 3 显示了同一对象在不同时间的不同情绪的图像分布。可以清楚地看到,这种差别比不同被试的差别要小得多:

表 1

表 2
表 1 是不同函数的参数量,表 2 是不同 copula 函数得到的欧几里得距离,较小的距离对应的 copula 函数拟合性较好,可以看到,frank copula 函数拟合性最好。
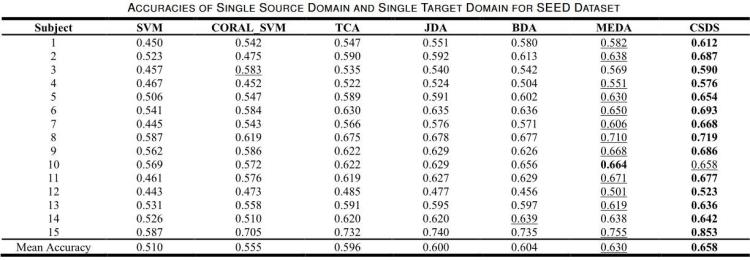
表 3
表 3 是不同方法在 seed 数据集中准确率的比较,可以看出作者提出的 csds 效果最好。
论文链接:https://ieeexplore.ieee.org/stamp/stamp.jsp?arnumber=10017294
撰稿人:陈希昶
审稿人:李景聪


